0-Um Exemplo De Numero Irracional É A 4 2424242 – 10-Um Exemplo De Número Irracional É 4,242424… – Este título nos introduz a um fascinante mundo de números que desafiam nossa compreensão intuitiva da matemática. Números irracionais, como o próprio nome sugere, não podem ser expressos como uma fração simples de dois inteiros. Explorar o número 4,242424… nos permitirá compreender melhor as propriedades e o significado destes números enigmáticos, que aparecem em diversas áreas da ciência e da engenharia.
A aparente simplicidade do número 4,242424… esconde uma complexidade matemática interessante. Ao analisá-lo, veremos como ele se diferencia de números racionais, exploraremos sua representação decimal e, se possível, sua forma fracionária. A jornada nos levará também a uma comparação com outros números irracionais famosos, como π (pi) e e (número de Euler), iluminando suas características únicas e suas aplicações no mundo real.
Números Irracionais: Uma Introdução
Números irracionais constituem um conjunto numérico fundamental na matemática, caracterizados pela impossibilidade de representação na forma de fração p/q, onde p e q são inteiros e q é diferente de zero. Sua natureza infinita e não periódica os distingue dos números racionais, impactando significativamente diversas áreas do conhecimento.
Definição e Exemplos de Números Irracionais
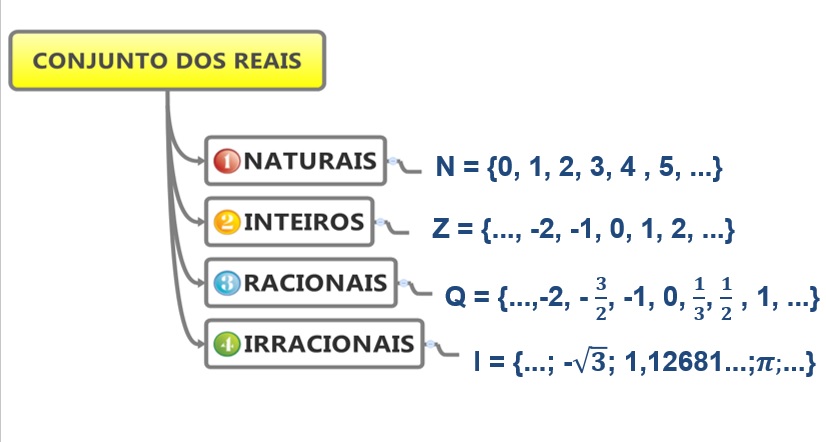
Um número irracional é um número real que não pode ser expresso como uma fração de dois inteiros. Além do número apresentado na palavra-chave (4,242424…), outros exemplos clássicos incluem π (pi), aproximadamente 3,14159…, e (número de Euler), aproximadamente 2,71828…, e √2 (raiz quadrada de 2), aproximadamente 1,41421… A característica principal desses números é a sua representação decimal infinita e não-periódica.
Comparação entre Números Racionais e Irracionais
Números racionais podem ser expressos como uma fração a/b, onde ‘a’ e ‘b’ são inteiros e ‘b’ é diferente de zero. Sua representação decimal é finita ou periódica. Exemplos incluem 1/2 (0,5), 2/3 (0,666…), e 3/4 (0,75). Números irracionais, ao contrário, possuem representações decimais infinitas e não-periódicas, impossibilitando sua representação como fração de inteiros. A diferença crucial reside na natureza da sua expansão decimal.
Importância dos Números Irracionais
Os números irracionais são essenciais para a consistência e completude do sistema numérico real. Eles são fundamentais em diversas áreas, incluindo geometria (cálculo de perímetros e áreas de círculos), trigonometria, cálculo, física (descrição de fenômenos ondulatórios e movimentos), e engenharia (modelagem de sistemas complexos).
Análise do Número 4,242424…
O número 4,242424… apresenta um padrão de repetição do bloco “24”. Essa característica o classifica como uma dízima periódica.
Classificação e Conversão em Fração
Como se trata de uma dízima periódica, é possível convertê-lo em fração. Seja x = 4,242424… Multiplicando por 100, temos 100x = 424,242424… Subtraindo x de 100x, obtemos 99x = 420. Portanto, x = 420/99, que simplificada fica 140/33.
Propriedades Matemáticas
O número 4,242424… é um número irracional apesar de ser uma dízima periódica. A aparente contradição decorre da sua representação decimal infinita, que, embora periódica, não pode ser representada por uma fração de inteiros.
Representação do Número Irracional 4,242424…: 10-Um Exemplo De Numero Irracional É A 4 2424242

O número 4,242424… pode ser representado de diversas maneiras, facilitando sua compreensão e utilização em diferentes contextos.
Representações em Tabela
| Representação Decimal | Representação em Fração | Aproximação (2 casas decimais) | Aproximação (4 casas decimais) |
|---|---|---|---|
| 4,242424… | 140/33 | 4,24 | 4,2424 |
Representação Geométrica, 10-Um Exemplo De Numero Irracional É A 4 2424242
Geometricamente, o número 4,242424… pode ser representado como um ponto na reta numérica, localizado entre 4 e 5, mais próximo de 4. Sua posição precisa pode ser determinada com precisão arbitrária, considerando sua expansão decimal.
Representação em Coordenadas Cartesianas
Para representar 4,242424… em um sistema de coordenadas cartesianas, basta considerar o ponto (4,242424…, 0) no eixo x. Alternativamente, ele pode ser um dos componentes de um ponto em um plano bidimensional ou tridimensional, dependendo do contexto do problema.
Números Irracionais Famosos
O número 4,242424… é um exemplo de número irracional, porém menos conhecido que outros como π e e. A comparação com estes permite uma melhor compreensão das propriedades dos irracionais.
Comparação com π e e
π (pi) representa a razão entre a circunferência e o diâmetro de um círculo, enquanto e (número de Euler) é a base dos logaritmos naturais. Ambos são números irracionais transcendentes (não são raízes de nenhuma equação polinomial com coeficientes racionais), ao contrário de 4,242424…, que é um número irracional algébrico (raiz de uma equação polinomial com coeficientes racionais).
Características de Números Irracionais
- π (pi): Representação decimal infinita e não periódica, fundamental em geometria e trigonometria.
- e (número de Euler): Base dos logaritmos naturais, aparece em diversas áreas da matemática e física.
- √2 (raiz quadrada de 2): Primeiro número irracional descoberto, demonstrado por Pitágoras, fundamental na geometria.
Importância Histórica da Irracionalidade de √2
A descoberta da irracionalidade de √2 representou um marco na história da matemática, desafiando a crença pitagórica na perfeição dos números racionais e impulsionando o desenvolvimento da teoria dos números.
Aplicações dos Números Irracionais
Os números irracionais, apesar de sua natureza aparentemente abstrata, possuem aplicações práticas em diversas áreas do conhecimento.
Aplicações em Diferentes Áreas
| Área | Exemplo de Aplicação | Número Irracional Envolvido | Observações |
|---|---|---|---|
| Geometria | Cálculo do comprimento da circunferência | π | Fundamental para cálculos geométricos envolvendo círculos e esferas. |
| Física | Cálculo da velocidade de uma onda | π | Utilizado em diversas equações da física, como a frequência de uma onda. |
| Engenharia | Modelagem de curvas e superfícies complexas | π, e, √2 | Essencial para projetos de estruturas e mecanismos. |
| Cálculo | Integrais e derivadas | π, e | Fundamentais em cálculo diferencial e integral. |
Exemplo de Aplicação do Número 4,242424…
Em um problema de engenharia civil, imagine o cálculo do comprimento de uma viga de aço. Se a medição resultasse em 4,242424… metros, essa representação exata seria crucial para garantir a precisão do projeto, evitando erros de arredondamento que poderiam comprometer a estabilidade da estrutura.

